now that we have a decent amount of tools to process lines, segments and triangles, it’s time to start using a paradoxically complex shape: Mister Circle.

the circle is basically a point and a radius yet if you look at this list of properties on wolfram circle, circles or on wikipedia circle, list of related topics you’ll understand that things are not that easy.

an exhaustive study of the circle is far beyond the scope of this series of articles and we’ll only take care of the most common ( and useful hopefully :) ) algorithms ; utilities that help us draw nice things or interact with circles.

in real life, if we have to draw one or many circles, we’ll use the graphics.drawCircle() methos of the API.
already lots of possibilities with this. click below to roll through 6 improvised variations:

( here’s the uber dirty class for the braves )

playing with circles is endless ( I mean, really ) so let’s focus on the tools.
a circle has very few properties : a position and a radius.
a portion of a circle is called an ARC and has some interesting features: showtime!

• just like mum, it is a point and has a radius: click drag and change the radius up there
• it has a startAngle, and an arcLength that define its length
• it can be rendered in 3 different ways: as an arc (…), as a sector aka pie chart or as a segment that uses a chord of the circle. NB if the sector is checked, the segment doesn’t work… cheap implementation… can be fixed… who cares
• while preparing this article, I found that a nice feature would be to have the possibility to invert the arc. you can do that with the checkbox
• another useful function is to know wether a point belongs to the arc or not, by checking the “closest point” checkbox, you’ll enabled this. the arc turns blue id the closest point to the mouse on the circle actually lies on the arc

NB the Arc class is using 1 to 8 curveTos rather than drawing a series of segments, this is both lighter and more elegant.
here’s a nice take at using curveTos, the one I used is supposed to be here but doesn’t seem available anymore.

that was fun already but the real fun comes when we put 2 circles together :)
hereunder is a circle-circle distance computation, a point-circle tangent computation, a circle-circle tangent computation and a circle contain circle test.

check the boxes and drag drop the circles around to see what happens.

• the circle-circle distance can be negative (and I can divide by zero \o/) it’s normal ; it indicates how deep the 2 circles interpenetrate. this negative length can be used to calculate a response of some kind.
• if you drag the smaller circle onto the other, it should turn pink and punch the shape of the smallest. this is the circle contain circle test
• the tangent points on a circle find the tangents of the red circle’s point onto the the black circle. I used the explanations given here. you can draw the arc formed between the 2 tangents and invert it to get a dropplet shape
• the circle-circle tangents finds the tangents of one circle onto the other. again I used a mix of the 2 articles here and there and ended up with something that does the thing. I love the capsule with the arcs turned on

those are really good tools to have in our computational backpack, the next 3 are probably the most useful though ; they’ll address the circle-circle intersection, the line-circle intersection and the segment-circle intersection.
that’s how it goes, it’s quite self explanatory I think, when line tests are enabled, you can drag the handles of the line.

• circles intersection performs a circle-circle intersection ; if the 2 circles intersect, it returns either 1 tangent point or the 2 points of the chord on which the circles intersect. I used the explanations here
• the line circle intersection will return either 0 point if no collision occured or 1 tangent point if the line is tangent to the circle or the 2 points of the chord ( secant in this case ) on which the line intersect the circle. took the code and explanations from here
• the segment circle intersection will do the same as th line circle test but use a segment instead of an infinite line. therefore you can get 2 intersection on a line test and 1 or none on the segment circle test. that can be very handy. I found ( after hours of search :/ ) and ported this code

NB it’s possible to test an ARC-LINE or ARC-SEGMENT intersection, by first computing the intersection points ips between the arc and the line and then performing an ArcUtils.isPointOnArc() for each resulting intersection point.

finally I’ve always been scared to death by the apollonius’ problem. don’t ask me why, there are things like that, a childish fear.
it says :

Given three objects, each of which may be a point, line, or circle, draw a circle that is tangent to each. There are a total of ten cases. The two easiest involve three points or three lines, and the hardest involves three circles.

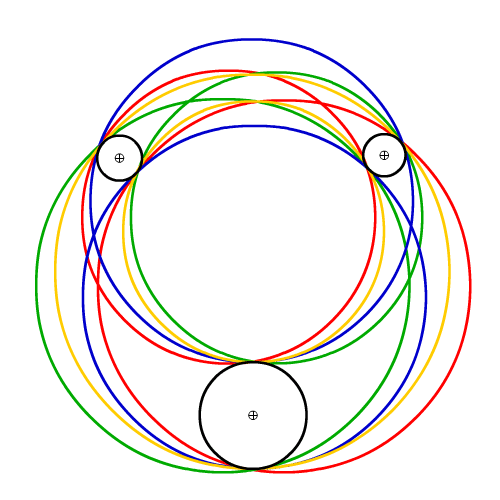
oh… that maybe why :)

actually the 3 dots solution is the circumcircle we’ve seen under the TRIANGLE section, the 3 lines, well I don’t really know but it can be an incircle of a triangle or using the point to circle tangents, it won’t be a big deal.

now three circles is the hardest case, the complexity looks incredible yet, as for all I’m trying to explain in this series of articles, complexity is an sum of simplicities. to address the Apollonius circles’ problem, I simply lacked the tools.
so I’ve read carefully the article and implemented the tools I needed namely:
- the radical line and the radical center
- the homothetics centers
- an inversion point method and inversion poles
so here they are!

we don’t have to understand how it works really, I don’t for instance, just followed the cookbook :)
anyway, we’re less interested in the maths behind than in the render in front.
notice that the radical line is the same as the circle-circle intersectio line.
tracing a point from an homothetic center will “scale” a point from one circle to the other.

so with this in hand, here’s the bugger I’ve been scared of for years:

notice the render 6 & 7 can really be useful. it’s not 100% stable ; if 2 circles have the same radius, it will not render (cheap tests… who cares).

and finally, a zip: BIGA_1.ZIP
update: the source code is available on google code

since the last drop, I refactored a lot, put the utils in the utils package, the shapes in the shapes package… and the samples of the above demos, in the samples/circle folder. I’ve also commented the GeomUtils and the CircleUtils in english..might help somehow ^^

there are very high chances that the previous LINE tests contained in the samples/lines folder won’t work un less you refactor the imports. if you’re lazy, use the source file from the previous article. fixed

next step:… well I ‘ll stop announcing the next steps ; I always fuck it up…
so : *surprise*

Tags: apollonius, circle, generative, generative art, geometry, intersection, introduction, line, segment